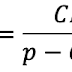Ejercicio resuelto punto muerto. SELECTIVIDAD CASTILLA Y LEÓN 2020 (examen extraordinaria septiembre)
Ejercicio resuelto punto muerto. SELECTIVIDAD CASTILLA Y LEÓN 2020 (examen extraordinaria septiembre)
ALTA SEGURIDAD S.A es una empresa dedicada a la instalación de alarmas en viviendas unifamiliares. Soporta unos costes fijos anuales de 150.000€. El departamento financiero tiene estimado que con un precio por instalación de 350€ alcanza su umbral de rentabilidad con la instalación de 1.000 unidades.
SE PIDE:
Calcular el coste variable partiendo de la situación dada y el número de instalaciones necesarias para alcanzar el umbral de rentabilidad si, manteniendo los costes iguales, se decide aumentar el precio de instalación a 400€. Representar gráficamente las dos situaciones.
Solución
El umbral de rentabilidad o punto muerto es el número de unidades que una empresa debe vender para poder recuperar todos sus costes, tanto los fijos como los variables. Si la empresa produce esa cantidad su beneficio será cero, ya que sus ingresos totales serán igual a sus costes totales.
Por tanto, planteamos la igualdad entre costes e ingresos.
IT = CT
Sabemos que los ingresos dependerán de la cantidad que vendamos (Q) y el precio de venta (P). El coste total será la suma de costes variables y fijos.
P·Q = CF + CV
Además, los costes variables los obtenemos multiplicando el coste variable unitario (Cvu) por la cantidad
P·Q = CF + CVu·Q
Si sustituimos datos llegamos a la fórmula que nos sabemos todos.
En este ejercicio lo podemos subdividir en dos apartados:
a) En el primero, lo que se nos pide es conocer el CVu, por lo que, sustituyendo en la fórmula anterior, lo podremos calcular:
Podemos comprobar como con esos datos si Q* = 1.000, se confirma que el beneficio es cero.
IT = P *Q = 350* 1000 = 350.000
CT = CF + CVu*Q = 150.000 + 200*1000 = 350.000
Vemos que en el puto muerto coincide que ingresos y costes son iguales y por tanto el beneficio es igual a cero.
b) En el segundo, se nos plantea cuál sería el umbral de rentabilidad en el caso de que el precio fuera de 400 y se mantuvieran constantes los costes:
Obviamente, en este segundo caso, al mantenerse los costes e incrementarse los precios, la empresa necesitará vender menos unidades para comenzar a obtener beneficios.
Podemos comprobar como con esos datos si Q* = 750, se confirma que el beneficio es cero.
IT = P *Q = 400* 750 = 300.000
CT = CF + CVu*Q = 150.000 + 200*750 = 300.000
Representación gráfica
Situación 1. Q* = 1.000
Situación 2. Q* = 1.000
Y aquí te dejo otro ejercicio de punto muerto para que puedas seguir practicando.
