Ejercicio resuelto TIR. SELECTIVIDAD (PAU) COMUNIDAD VALENCIANA 2021 (examen extraordinaria julio)
Ejercicio resuelto TIR. SELECTIVIDAD (PAU) COMUNIDAD VALENCIANA 2021 (examen extraordinaria julio)
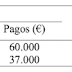
Una empresa está estudiando la viabilidad de dos proyectos de inversión. Cada uno de los proyectos requiere de 45.000 euros de desembolso inicial y se prevén los siguientes cobros y pagos a lo largo de la vida de los proyectos:
a) Para cada proyecto, calcule los flujos netos de caja de cada año. (Hasta 0,4 puntos)
b) Calcule la tasa interna de rentabilidad de cada uno de los proyectos. (Hasta 1 punto)
c) Determine la viabilidad de cada uno de los proyectos si la tasa de descuento es igual a 5,5%. Razone su respuesta. (Hasta 0,6 puntos)
Solución
a) Flujos netos de caja
Los flujos netos de caja los calculamos como la diferencia entre cobros y pagos de cada año.
Proyecto 1
FNC 1 = 95.000 – 60.000 = 35.000
FNC 2 = 45.000 – 32.500 = 12.500
Proyecto 2
FNC 1 = 52.000 – 37.000 = 15.000
FNC 2 = 80.000 – 45.000 = 35.000
b) Cálculo TIR
La TIR (tasa interna de rentabilidad) nos indica cual debería ser la tasa de actualización que hace el VAN sea igual a 0. Es decir, la TIR tiene que ser mayor a la rentabilidad mínima por la que un proyecto nos sería rentable. A mayor TIR mayor rentabilidad.
Proyecto 1
Si multiplicamos por (1+TIR)2 a todos los elementos de la ecuación nos queda que:
- 45.000 (1+TIR)2 + 35.000 (1+TIR) + 12.500
Si suponemos que (1+TIR) es igual a X
- 45.000 x2 + 35.000 x + 12.500
Por lo que nos queda una ecuación de segundo grado
Donde el primer elemento elevado al cuadrado es ”a” (-45.000) el segundo elevado a 1 es “b” (35.000) y el independiente es “c” (12.500).
El único resultado que tiene sentido en este caso es el positivo (no puede ser rentabilidad negativa para un proyecto).
Recuerda que dijimos que:
x = 1+TIR
TIR = 1,0438 - 1 = 0,0438
Si lo multiplicamos por 100 para hacerlo un porcentaje, entonces tenemos 4,38%.
Lo cual quiere decir que para el proyecto la TIR = 4,38% y por tanto esa es la tasa de rentabilidad que iguala el VAN a cero. Siempre que la TIR sea mayor al valor “k” nuestro proyecto será rentable ya que en ese caso el VAN será positivo.
Proyecto 2
Si multiplicamos por (1+TIR)2 a todos los elementos de la ecuación nos queda que:
- 45.000 (1+TIR)2 + 15.000 (1+TIR) + 35.000
Si suponemos que (1+TIR) es igual a X
- 45.000 x2 + 15.000 x + 35.000
Y por tanto
Como ya sabemos
x = 1+TIR
TIR = 1,0642 - 1 = 0,0642
Si lo multiplicamos por 100 para hacerlo un porcentaje, entonces tenemos 6,42%
Lo cual quiere decir que para el proyecto la TIR = 6,42% y por tanto esa es la tasa de rentabilidad que iguala el VAN a cero.
c) Viabilidad del proyecto
Siempre que la TIR sea mayor al valor “k” nuestro proyecto será rentable ya que en ese caso el VAN será positivo.
Proyecto 1
Como la TIR (4,38%) < k (5,5%), el proyecto NO es rentable.
Proyecto 2
Como la TIR (6,42%) > k (5,5%), el proyecto SÍ es rentable.
Y si quieres seguir repasando.