Ejercicio resuelto VAN, payback y TIR. MODELO DE EXAMEN 2020 SELECTIVIDAD MADRID (Evau)
Ejercicio resuelto VAN, payback y TIR. MODELO DE EXAMEN 2020 SELECTIVIDAD MADRID (Evau)
A una empresa se le presentan dos posibilidades de inversión, la Opción 1 y la Opción 2. Si se realiza la inversión de la Opción 1 es necesario un desembolso inicial de 20.000 euros y los flujos de caja esperados son de 11.000 euros el primer año y de 12.000 euros el segundo. Por otra parte, la Opción 2 supone un desembolso inicial de 30.000 euros y los flujos de caja esperados son de 15.000 euros el primer año y de 16.000 euros el segundo. Se pide, para una tasa de descuento del 8% anual:
a) Calcule el Plazo de Recuperación o “Pay-Back”, el Valor Actual Neto (VAN) y la Tasa Interna de Rentabilidad (TIR) de la Opción 1. Indique si la Opción 1 es aceptable según los criterios del VAN y TIR (1 punto).
b) Calcule el Plazo de Recuperación o “Pay-Back”, el Valor Actual Neto (VAN) y la Tasa Interna de Rentabilidad (TIR) de la Opción 2. Indique si la Opción 2 es aceptable según los criterios del VAN y TIR (1 punto).
Solución
a) Payback Proyecto 1
Con el Pay-Back tenemos que sumar los FNC hasta recuperar la inversión inicial (20000). Cuando lo hagamos, calcularemos el momento exacto del año en el que se produce dicha recuperación
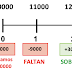
Como el desembolso inicial son 20000 en el año 0 esa es la cantidad que falta por recuperar. Al recuperar 9000 el año 1, todavía faltan 11000 (que ponemos con saldo negativo). Sin embargo, en el año 2 al recuperar 12000, vemos que ya hemos recuperado todo y además sobran 3000 (que ponemos con signo positivo).
El momento en el que recuperemos todo (los 20000), será el plazo de recuperación. Lo normal, como vemos es que recuperemos en medio de un año y otro. Ese punto es cuando la cantidad pendiente de recuperar pasa de negativa a positiva.
Vemos que recupera su inversión inicial entre el año 1 y 2, ya que a final del año 1 quedaban por recuperar 9000, y a final del año 2 la cifra pasa a +3000 (hemos recuperado todo y nos sobra). Entre el año 1 y 2 la cifra de pendiente de recuperar pasa de negativa (-9000) a positiva (+3000).
Para saber el momento exacto que recuperamos la inversión entre el año 1 y 2, suponemos que los 12000 euros del año 2, cuando recuperamos más del desembolso inicial se reciben a lo largo del año (cogemos el año comercial de 360 días), y queremos saber cuántos días tardará en recuperar los 9000 que le faltaban.
Por tanto, tenemos en cuenta dos puntos.
1. Cuanto dinero generé el año que recuperé el dinero y me sobró (año 212000)
2. Cuánto dinero faltaba por recuperar justo el año antes de conseguirlo (año 19000)
Genera 12000------ 360 días
Faltan 9000-------- x días
X = (9000*360) / 12000 = 270 días
Pay back 1 = Tarda en recuperar la inversión 1 año y 270 días
El proyecto es realizable ya que recupera la inversión
VAN proyecto 1.
Consiste en actualizar todos los flujos netos de caja al momento actual. Es decir, tenemos que calcular cuánto valdrían todos los flujos netos de caja (FNC) en el momento 0. Para ello utilizamos el método de la actualización que consisten en dividir cada FNC entre (1+k)n, donde la n minúscula nos indica la cantidad de años que tenemos que actualizar.
TIR proyecto 1.
La TIR (tasa interna de rentabilidad) nos indica cual debería ser la tasa de actualización que hace el VAN sea igual a 0. Es decir, la TIR tiene que ser mayor a la rentabilidad mínima por la que un proyecto nos sería rentable. A mayor TIR mayor rentabilidad.
Teniendo en cuenta los datos que nos da el ejercicio;
:
- 20.000 (1+TIR)2 + 11.000 (1+TIR) + 12.000
Si suponemos que (1+TIR) es igual a X
- 20.000 x2 + 11.000 x + 12.000
Por lo que nos queda una ecuación de segundo grado
Donde el primer elemento elevado al cuadrado es ”a” (-20.000) el segundo elevado a 1 es “b” (11.000) y el independiente es “c” (12.000).
El único resultado que tiene sentido en este caso es el positivo (no puede ser rentabilidad negativa para un proyecto)
Recuerda que dijimos que:
x = 1+TIR
TIR = 1,0969- 1 = 0,0969
Si lo multiplicamos por 100 para hacerlo un porcentaje, entonces tenemos 9,69%
Lo cual quiere decir que para el proyecto la TIR = 9,69% y por tanto esa es la tasa de rentabilidad que iguala el VAN a cero. Siempre que la TIR ese caso el VAN será positivo.
Como en nuestro caso TIR (9,69%) > k (8%), el proyecto es rentable.
b) Payback proyecto 2
Vemos que recupera su inversión inicial entre el año 1 y 2, ya que a final del año 1 quedaban por recuperar 15000 y a final del año 2 la cifra pasa a +1000 (hemos recuperado todo y nos sobra). Entre el año 1 y 2 la cifra de pendiente de recuperar pasa de negativa (-15000) a positiva (+1000).
Para saber el momento exacto que recuperamos la inversión entre el año 1 y 2, suponemos que los 16000 euros del año 2, cuando recuperamos más del desembolso inicial se reciben a lo largo del año (360 días), y queremos saber cuántos días tardará en recuperar los 15000 que le faltaban.
Por tanto, tenemos en cuenta dos puntos.
1. Cuanto dinero generé el año que recuperé el dinero y me sobró (año 216000)
2. Cuánto dinero faltaba por recuperar justo el año antes de conseguirlo (año 115000)
Genera 16000------ 360 días
Faltan 15000-------- x días
X = (16000*360) / 16000 = 337,5 días
Pay back 2 = Tarda en recuperar la inversión 1 año y 337,5 días
VAN proyecto 2
TIR proyecto 2
Teniendo en cuenta los datos que nos da el ejercicio;
Si multiplicamos por (1+TIR)2 a todos los elementos de la ecuación nos queda que:
- 30.000 (1+TIR)2 + 15.000 (1+TIR) + 16.000
Si suponemos que (1+TIR) es igual a X
- 30.000 x2 + 15.000 x + 16.000
Donde el primer elemento elevado al cuadrado es ”a” (-30.000) el segundo elevado a 1 es “b” (15.000) y el independiente es “c” (16.000).
El único resultado que tiene sentido en este caso es el positivo (no puede ser rentabilidad negativa para un proyecto)
Recuerda que dijimos que:
x = 1+TIR
TIR = 1,0219 - 1 = 0,0219
Si lo multiplicamos por 100 para hacerlo un porcentaje, entonces tenemos 2,19%
Lo cual quiere decir que para el proyecto la TIR = 2,19% y por tanto esa es la tasa de rentabilidad que iguala el VAN a cero. Siempre que la TIR (2,19%) sea mayor al tipo de interés k, nuestro proyecto será rentable ya que en ese caso el VAN será positivo.
Como en nuestro caso TIR (2,19%) < k (8%), el proyecto NO es rentable.