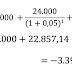Ejercicio resuelto VAN y TIR. SELECTIVIDAD MADRID (Evau) 2019 (examen extraordinaria julio)
Ejercicio resuelto VAN y TIR. SELECTIVIDAD MADRID 2019 (examen extraordinaria julio)
La empresa BKES produce bicicletas y se está planteando la fabricación de patinetes eléctricos. Para valorar sus posibilidades estudia un proyecto que requiere una inversión inicial de 58.000 euros y estima que el flujo neto de caja del primer año será de 24.000 euros y el del segundo año de 35.000 euros. Sabiendo que el coste de capital de la empresa es del 5% anual, se pide:
a) Calcule el Valor Actual Neto (VAN) (0,75 puntos) y la Tasa Interna de Rentabilidad (TIR) (0,75 puntos) de la inversión.
b) Explique si la inversión es aceptable según el criterio del VAN (0,25 puntos).
c) Explique si la inversión es aceptable según el criterio de la TIR (0,25 puntos).
Solución
a) Cálculo del VAN y la TIR
VAN
Consiste en actualizar todos los flujos netos de caja al momento actual. Es decir, tenemos que calcular cuánto valdrían todos los flujos netos de caja (FNC) en el momento 0. Para ello utilizamos el método de la actualización que consisten en dividir cada FNC entre (1+k)n, donde la n minúscula nos indica la cantidad de años que tenemos que actualizar.
TIR
La TIR (tasa interna de rentabilidad) nos indica cual debería ser la tasa de actualización que hace el VAN sea igual a 0. Es decir, la TIR tiene que ser mayor a la rentabilidad mínima por la que un proyecto nos sería rentable. A mayor TIR mayor rentabilidad.
Teniendo en cuenta los datos que nos da el ejercicio;
Si multiplicamos por (1+TIR)2 a todos los elementos de la ecuación nos queda que:
- 58.000 (1+TIR)2 + 24.000 (1+TIR) + 35.000
Si suponemos que (1+TIR) es igual a X
- 58.000 x2 + 24.000 x + 35.000
Por lo que nos queda una ecuación de segundo grado
Donde el primer elemento elevado al cuadrado es ”a” (-58.000) el segundo elevado a 1 es “b” (24.000) y el independiente es “c” (35.000).
El único resultado que tiene sentido en este caso es el positivo (no puede ser rentabilidad negativa para un proyecto)
Recuerda que dijimos que:
x = 1+TIR
TIR = 1,01079- 1 = 0,01079
Si lo multiplicamos por 100 oara hacerlo un porcentaje, entonces tenemos:
TIR = 1,079%
Lo cual quiere decir que para el proyecto la TIR = 1,079% y por tanto esa es la tasa de rentabilidad que iguala el VAN a cero. Siempre que la TIR (1,079%) sea mayor al tipo de interés k, nuestro proyecto será rentable ya que en ese caso el VAN será positivo.
b) Proyecto rentable según el VAN
Como el VAN es menor que 0 (-3.396,83) el proyecto no es rentable según este método
c) Proyecto rentable según TIR
Como la TIR (1,079%) es inferior al coste del capital (k=5%) el proyecto tampoco será rentable por este método.